Caractéristique d'un dipôle

Programme de seconde générale et technologique 2019.

"Représenter un nuage de points associé à la caractéristique d’un dipôle et modéliser la caractéristique de ce dipôle à l’aide d’un langage de programmation".

Principe

Tracer le nuage de points des mesures de la tension et de l'intensité du courant d'un dipôle électrique.
Modéliser cette caractéristique quand cela est possible.

Exemple 1 : caractéristique d'une résistance

Les mesures de l'intensité du courant \(I\) et de la tension \(U\) aux bornes d'une résistance de \(220~\Omega\) à 5% sont données dans le tableau ci-dessous.

Mesure	1	2	3	4	5	6	7	8	9	10
I (mA)	0	51	101	151	203	252	303	356	406	456
U (V)	0	1,11	2,22	3,28	4,42	5,5	6,68	7,73	8,92	9,91

Tracé du nuage de points

import matplotlib.pyplot as plt

# MESURES
I = [0., 0.0051, 0.0101, 0.0151, 0.0203, 0.0252, 0.0303, 0.0356, 0.0406, 0.0456]
U = [0., 1.11  , 2.22  , 3.28  , 4.42  , 5.5   , 6.68  , 7.73  , 8.92  , 9.91  ]

# CARACTERISTIQUE
plt.plot(I, U, "r+")
plt.title("Caractéristique d'une résistance")
plt.xlabel("I (A)")
plt.ylabel("U (V)")
plt.grid()
plt.show()

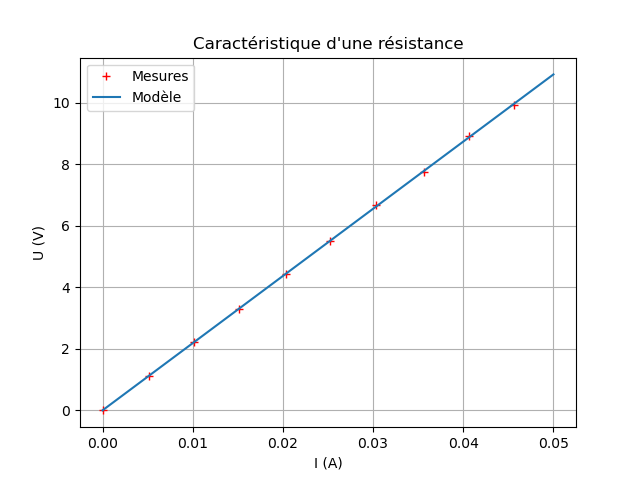
Modélisation avec `scipy.stats.linregress()`

Régression linéaire par la méthode des moindres carrés.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import linregress

# MESURES
I = [0., 0.0051, 0.0101, 0.0151, 0.0203, 0.0252, 0.0303, 0.0356, 0.0406, 0.0456]
U = [0., 1.11  , 2.22  , 3.28  , 4.42  , 5.5   , 6.68  , 7.73  , 8.92  , 9.91  ]

# MODELISATION
a, b, _, _, _ = linregress(I, U)
print("a =", a)
print("b =", b)
print("R =", round(a), "Ohm")

# CONSCTRUCTION DU MODELE
I_mod = np.array([0, 0.05])
U_mod = a*I_mod + b

# COURBE
plt.plot(I, U, "r+", label="Mesures")
plt.plot(I_mod, U_mod, label="Modèle")
plt.legend()
plt.title("Caractéristique d'une résistance")
plt.xlabel("I (A)")
plt.ylabel("U (V)")
plt.grid()
plt.show()

>>> %Run
a = 218.29027146901586
b = 0.0021647132211279896
R = 218 Ohm

Modélisation avec `numpy.polyfit()`

La régression linéaire avec numpy.polyfit() donne le même résultat.

import numpy as np
import matplotlib.pyplot as plt

# MESURES
I = [0., 0.0051, 0.0101, 0.0151, 0.0203, 0.0252, 0.0303, 0.0356, 0.0406, 0.0456]
U = [0., 1.11  , 2.22  , 3.28  , 4.42  , 5.5   , 6.68  , 7.73  , 8.92  , 9.91  ]

# MODELISATION
a, b = np.polyfit(I, U, 1)
print("a =", a)
print("b =", b)
print("R =", round(a), "Ohm")

# CONSCTRUCTION DU MODELE
I_mod = np.array([0, 0.05])
U_mod = a*I_mod + b

# COURBE
plt.plot(I, U, "r+", label="Mesures")
plt.plot(I_mod, U_mod, label="Modèle")
plt.legend()
plt.title("Caractéristique d'une résistance")
plt.xlabel("I (A)")
plt.ylabel("U (V)")
plt.grid()
plt.show()

>>> %Run
a = 218.29027146901592
b = 0.002164713221130428
R = 218 Ohm

Modélisation avec `scipy.optimize.curve_fit()`

Une modélisation à partir d'une fonction linéaire est plus adaptée au nuage de points obtenu.

\[f(x) = a \times x\]

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# MESURES
I = [0., 0.0051, 0.0101, 0.0151, 0.0203, 0.0252, 0.0303, 0.0356, 0.0406, 0.0456]
U = [0., 1.11  , 2.22  , 3.28  , 4.42  , 5.5   , 6.68  , 7.73  , 8.92  , 9.91  ]

# DEFINITION DE LA FONCTION
def fct(x, a):
      return a*x         # Expression du modèle

# MODELISATION
(a), _ = curve_fit(fct, I, U)   # Détermination des paramètres du modèle
print("a =", a)
print("R =", round(a[0]), "Ohm")

# CONSCTRUCTION DU MODELE
I_mod = np.array([0, 0.05])
U_mod = a*I_mod

# COURBE
plt.plot(I, U, "r+", label="Mesures")
plt.plot(I_mod, U_mod, label="Modèle")
plt.legend()
plt.title("Caractéristique d'une résistance")
plt.xlabel("I (A)")
plt.ylabel("U (V)")
plt.grid()
plt.show()

>>> %Run
a = [218.35770119]
R = 218 Ohm

Exemple 2 : caractéristique d'une CTN

Nous considérons maintenant un capteur non linéaire. Il s'agit d'un CTN de 10K du type EKS 221. Le tableau ci-dessous donne les mesures de la température en fonction de la résistance électrique de ce capteur.

Mesure	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
T (°C)	2	6	10	15	20	25	30	35	40	45	50.1	55	60	65	70	75	80	85
R (Ohm)	25378	21487	18301	14990	12402	10295	8615	7226	1630	1404	6097	5121	4306	3632	3070	2609	2221	1903

Nuage de points

import matplotlib.pyplot as plt

# DONNEES
T = [2, 6, 10, 15, 20, 25, 30, 35, 40, 45, 50.1, 55, 60, 65, 70, 75, 80, 85]
R = [25378,21487,18301,14990,12402,10295,8615,7226,6097,5121,4306,3632,3070,2609,2221,1903,1630,1404]

# COURBE
plt.plot(R, T, "r+")                    # Tracé du nuage de points en rouge
plt.title("Caractéristique d'une CTN")  # Ajout d'un titre
plt.xlabel("R (Ohm)")                   # Ajout d'une légende sur l'abscisse
plt.xlim(0, 30000)                      # Echelle en abscisse
plt.ylabel("T (°C)")                    # Ajout d'une légende sur l'ordonnée
plt.ylim(0, 90)                         # Echelle en ordonnée
plt.grid()                              # Ajoute une grille
plt.show()                              # Affiche la figure

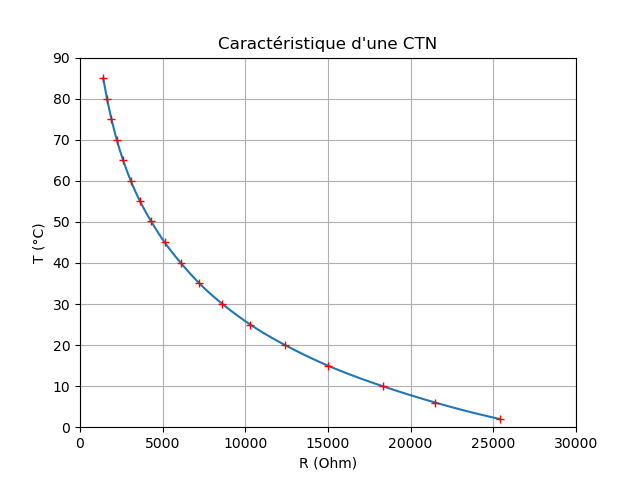
Modélisation par une interpolation avec `scipy.interpolate.interp1d()`

Il est possible de modéliser la caractéristique de ce capteur par une interpolation et obtenir ainsi une fonction d'étalonnage de la CTN.

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

# DONNEES
T = [2, 6, 10, 15, 20, 25, 30, 35, 40, 45, 50.1, 55, 60, 65, 70, 75, 80, 85]
R = [25378,21487,18301,14990,12402,10295,8615,7226,6097,5121,4306,3632,3070,2609,2221,1903,1630,1404]

# INTERPOLATION
f = interp1d(R, T, kind='cubic')

# CONSTRUCTION DU MODELE
R_int = np.linspace(1404, 25378, 100)
T_int = f(R_int)

# COURBE
plt.plot(R_int, T_int)
plt.plot(R, T, "r+")                    # Tracé du nuage de points en rouge
plt.title("Caractéristique d'une CTN")  # Ajout d'un titre
plt.xlabel("R (Ohm)")                   # Ajout d'une légende sur l'abscisse
plt.xlim(0, 30000)                      # Echelle en abscisse
plt.ylabel("T (°C)")                    # Ajout d'une légende sur l'ordonnée
plt.ylim(0, 90)                         # Echelle en ordonnée
plt.grid()                              # Ajoute une grille
plt.show()                              # Affiche la figure

Utilisation de la courbe d'étalonnage ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ééééé

Il est intéressant de noter que la fonction f() retourne par interpolation la valeur de la température du capteur pour n'importe quelle valeur de la résistance dans la plage de mesure.

Le programme suivant donne la température à partir d'une mesure à l'ohmmètre de la résistance de la CTN.

from scipy.interpolate import interp1d

# DONNEES
T = [2, 6, 10, 15, 20, 25, 30, 35, 40, 45, 50.1, 55, 60, 65, 70, 75, 80, 85]
R = [25378,21487,18301,14990,12402,10295,8615,7226,6097,5121,4306,3632,3070,2609,2221,1903,1630,1404]

# INTERPOLATION
f = interp1d(R, T, kind='cubic')

# SAISIE ET CALCUL
while True:
   res = float(input("R (Ohm) = "))  # Saisie de la résistance
   if res == 0:                      #
      break                          # Stop de la boucle pour R = 0
   temp = f(res)                     # Caclul de la température
   print("T (°C) =", temp)           # Affichage

print("Fin !")

>>> %Run
R (Ohm) = 10000
T (°C) = 25.806756762710716
R (Ohm) = 15000
T (°C) = 14.982769995915337
R (Ohm) = 20000
T (°C) = 7.788406834764948
R (Ohm) = 0
Fin !

Note

Il est envisageable de mesurer la résistance de la CTN automatiquement par un micro-contrôleur programmé en Python et d'en déduire la température.