Résolution d'une équation différentielle avec la méthode d'Euler implicite (CPGE)
Équation différentielle d'ordre 1
Soit l'équation différentielle de la forme suivante :
\[\tau \cdot y'(t) + y(t) = g(t)\]
qui peut également s'écrire comme suit :
\[y'(t) = \dfrac{g(t)-y(t)}{\tau}\]
ou plus généralement :
\[\boxed{y'(t) = F(y(t), t)}
\hspace{1cm}\text{avec}\hspace{1cm}
F(y(t), t) = \dfrac{g(t_n)-y(t_n)}{\tau}\]
Méthode d'Euler implicite
En 1770, Euler propose une approximation de la dérivée :
\[y'(t_n) \approx\dfrac{y(t_{n+1})-y(t_n)}{h}
\hspace{1cm}\text{avec}\hspace{1cm}
h = t_{n+1}-t_{n}\]
qui donne la relation suivante :
\[y(t_{n+1}) \approx y(t_n) + h \cdot y'(t_n)
\hspace{1cm}\text{ou encore}\hspace{1cm}
\boxed{y(t_{n+1}) \approx y(t_n) + h \cdot F(y(t), t)}\]
On obtient ainsi une équation de récurrence :
\[\begin{split}\left \{
\begin{array}{l}
y_{n+1} \approx y_n + h \cdot F(y_n, t_n)
\hspace{.5cm}\text{pour}\hspace{.5cm}
n=0,1,...,N \\
y_0 = y(0)
\end{array}
\right.\end{split}\]
A l'instant initial \(t=0\), on a \(y(0)=y_0\).
Implémentation d'une fonction euler
import numpy as np
import matplotlib.pyplot as plt
def derive(y, t):
if t<T/2:
g = 10
else:
g = 6
return (g-y)/tau
def euler(derive, y0, t):
h = t[1]-t[0]
N = len(t)
y = np.zeros(N)
y[0] = y0
for n in range(0,N-1):
y[n+1] = y[n] + h*derive(y[n], t[n])
return y
# PARAMETRES
tau = 2
T = 20
N = 1000
# RESOLUTION DE L'EQUADIFF
y0 = 2 # Condition initiale
t = np.linspace(0,T,N) # Tableau du temps
y = euler(derive, y0, t) # Integration
# COURBES
plt.plot(t, y, ".", ms =2 ,label='y(t) pour N={}'.format(N))
plt.legend()
plt.xlabel('t')
plt.ylim(0,12)
plt.ylabel('y')
plt.grid()
plt.show()
La fonction d'intégration euler :
détermine le pas
het le nombre de pointsN.pose la condition initiale
y[0] = y0.calcule les termes
y[n+1]par récurrence dans une boucle deNitérations.
La fonction derive caractérise ici l'équation différentielle prise comme exemple.
- Résultats
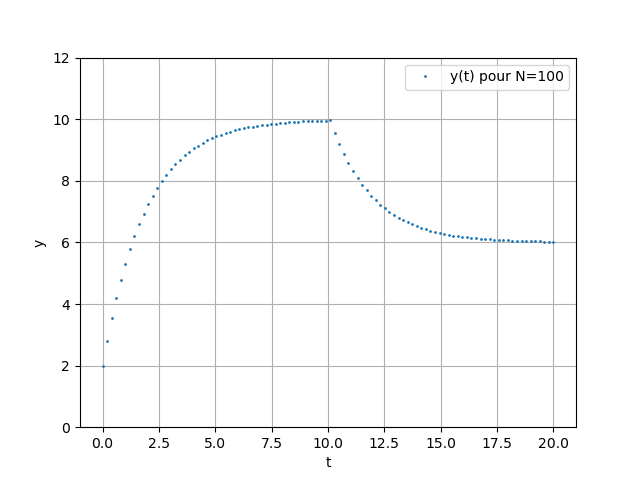
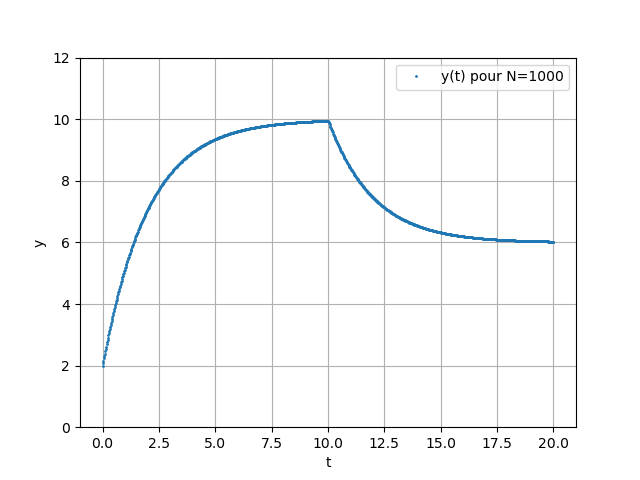
Avec la fonction odeint
La fonction odeint de scipy.integrate utilise une autre méthode d'intégration plus précise que celle d'Euler.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
def derive(y, t):
if t<T/2:
g = 10
else:
g = 6
return (g-y)/tau
# PARAMETRES
tau = 2
T = 20
N = 100
# RESOLUTION DE L'EQUADIFF
y0 = 2 # Condition initiale
t = np.linspace(0,T,N) # Tableau du temps
y = odeint(derive, y0, t)
# COURBES
plt.plot(t, y, ".", ms =2 ,label='y(t) pour N={}'.format(N))
plt.legend()
plt.xlabel('t')
plt.ylim(0,12)
plt.ylabel('y')
plt.grid()
plt.show()
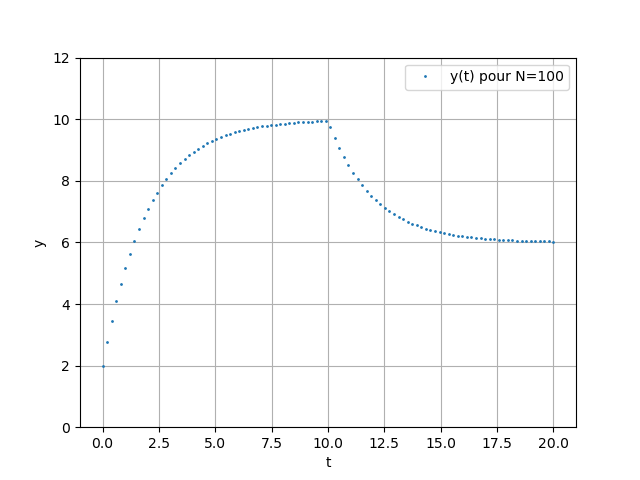
\(N=100\)