Correction des exercices
Exercice 1. (dilution)
On sait que :
\[F=\dfrac{C_m}{C_f}
\hspace{1cm}\text{et}\hspace{1cm}
V_m = \dfrac{V_f}{F}\]
Cm = 30 # (g/L) concemtration massique solution mère
Cf = 10 # (g/L) concentration massique solution fille
Vf = 500 # (mL) Volume solution fille
F = Cm/Cf # (--) Calcul du facteur de dilution
Vm = Vf/F # (mL) Calcul de Vm
Veau = Vf-Vm # (mL) Calcul de Veau (volume d'eau à compléter)
# AFFICHAGE
print("Prélever ", round(Vm,0), " mL de solution mère.")
print("Puis ajouter", round(Veau,0), "mL d'eau pour obtenir", round(Vf,0), "mL de solution fille")
print("Le facteur de dilution est de", round(F,2))
Ou avec l'affichage du texte avec la méthode format du type str.
Cm = 30 # (g/L) concemtration massique solution mère
Cf = 10 # (g/L) concentration massique solution fille
Vf = 500 # (mL) Volume solution fille
F = Cm/Cf # (--) Calcul du facteur de dilution
Vm = Vf/F # (mL) Calcul de Vm
Veau = Vf-Vm # (mL) Calcul de Veau (volume d'eau à compléter)
# AFFICHAGE
print("Prélever {:.0f} mL de solution mère.".format(Vm))
print("Puis ajouter {:.0f} mL d'eau pour obtenir {:.0f} mL de solution fille".format(Veau, Vf))
print("Le facteur de dilution est de {:.1f}".format(F))
Exercice 2. (distance focale)
f_prim = [19.1, 18.9, 18.7, 19.0, 18.9, 19.2, 18.8, 18.7] # Listes des mesures
nb = len(f_prim) # Nombre de mesures
moyenne = sum(f_prim)/len(f_prim) # Moyenne
maximum = max(f_prim) # Maximum
minimum = min(f_prim) # Minimum
f_prim.pop(0) # supprime la première mesure
f_prim.pop() # supprime la dernière mesure (-1 par défaut)
# OU
#f_prim = f_prim[1:-1] # supprime la première et la dernière
Exercice 3. (célérité son)
c = [335, 338, 341, 339, 340, 336, 343, 337, 341, 339, 337] # (m/s) célérité son
somme = 0
for i in range(len(c)):
somme = somme + c[i]
moyenne = somme/len(c)
print("Moyenne =", moyenne)
Exercice 4. (vitesse)
A partir d'une liste v vide au départ.
t = [0. , 0.04, 0.08, 0.12, 0.16, 0.20, 0.24, 0.28, 0.32, 0.36, 0.40, 0.44, 0.48] # (s)
z = [1.66, 1.61, 1.53, 1.45, 1.35, 1.23, 1.10, 0.96, 0.79, 0.61, 0.42, 0.21, 0. ] # (m)
v = []
for i in range(1, len(t)-1):
V = -(z[i+1]-z[i-1])/(t[i+1]-t[i-1]) # (m/s) Calcul la vitesse en cours
v.append(round(V,2)) # (m/s) Mémorisation de la vitesse
print(v)
>>> %Run
[1.62, 2.0, 2.25, 2.75, 3.13, 3.37, 3.88, 4.38, 4.62, 5.0, 5.25]
Attention à la taille de la liste v à la fin !
Ou à partir d'une liste v initialisée par N zéros.
t = [0. , 0.04, 0.08, 0.12, 0.16, 0.20, 0.24, 0.28, 0.32, 0.36, 0.40, 0.44, 0.48] # (s)
z = [1.66, 1.61, 1.53, 1.45, 1.35, 1.23, 1.10, 0.96, 0.79, 0.61, 0.42, 0.21, 0. ] # (m)
N = len(t) # Taille de la liste
v = [0]*N # Création d'une liste de 0 de taille N
for i in range(1, N-1):
v[i] = round(-(z[i+1]-z[i-1])/(t[i+1]-t[i-1]), 2) # (m/s) Calcul la vitesse en cours
print(v)
>>> %Run
[0, 1.62, 2.0, 2.25, 2.75, 3.13, 3.37, 3.88, 4.38, 4.62, 5.0, 5.25, 0]
Exercice 5. (énergies)
z = [1.61, 1.53, 1.45, 1.35, 1.23, 1.10, 0.96, 0.79, 0.61, 0.42, 0.21] # (m)
v = [1.58, 1.95, 2.27, 2.69, 3.12, 3.49, 3.91, 4.38, 4.65, 4.91, 5.23] # (m/s)
Epp, Ec, Em = [], [], [] # Initialisations des tableaux
m = 55E-3 # (kg) Masse de la balle
g = 9.81 # (m/s²) Accélération de pesanteur
for i in range(len(z)):
EPP = m*g*z[i] # Calcul l'énergie potentielle de pesanteur en cours
EC = 0.5*m*v[i]**2 # Calcul l'énergie cinétique en cours
Epp.append(round(EPP,3)) # Complète le tableau Epp
Ec.append(round(EC,3)) # Complète le tableau Ec
Em.append(round(EPP+EC,3)) # Complète le tableau Em
# AFFICHAGE
print("Epp (J) :", Epp)
print("Ec (J) :", Ec)
print("Em (J) :", Em)
>>> %Run
Epp (J) : [0.869, 0.826, 0.782, 0.728, 0.664, 0.594, 0.518, 0.426, 0.329, 0.227, 0.113]
Ec (J) : [0.069, 0.105, 0.142, 0.199, 0.268, 0.335, 0.42, 0.528, 0.595, 0.663, 0.752]
Em (J) : [0.937, 0.93, 0.924, 0.927, 0.931, 0.928, 0.938, 0.954, 0.924, 0.89, 0.866]
Exercice 6. (énergies)
z = [1.61, 1.53, 1.45, 1.35, 1.23, 1.10, 0.96, 0.79, 0.61, 0.42, 0.21] # (m)
v = [1.58, 1.95, 2.27, 2.69, 3.12, 3.49, 3.91, 4.38, 4.65, 4.91, 5.23] # (m/s)
m = 55E-3 # (kg) Masse de la balle
g = 9.81 # (m/s²) Accélération de la pesanteur
Epp = [m*g*Z for Z in z] # Tableau des énergies potentielles de pesanteur
Ec = [0.5*m*V**2 for V in v] # Tableau des énergies cinétiques
Em = [Epp[i]+Ec[i] for i in range(len(z))] # Tableau des énergies mécaniques
# AFFICHAGE
print("Epp (J) :", Epp)
print("Ec (J) :", Ec)
print("Em (J) :", Em)
>>> %Run
Epp (J) : [0.8686755000000002, 0.8255115000000002, 0.7823475000000001, 0.7283925000000001, 0.6636465000000001, 0.5935050000000002, 0.5179680000000001, 0.4262445000000001, 0.32912550000000007, 0.22661100000000003, 0.11330550000000002]
Ec (J) : [0.06865100000000002, 0.10456874999999999, 0.14170475, 0.19899275, 0.26769600000000005, 0.33495275, 0.42042275000000007, 0.527571, 0.5946187500000001, 0.66297275, 0.7522047500000002]
Em (J) : [0.9373265000000002, 0.9300802500000002, 0.9240522500000001, 0.9273852500000002, 0.9313425000000002, 0.9284577500000002, 0.9383907500000002, 0.9538155000000001, 0.9237442500000002, 0.88958375, 0.8655102500000003]
ou
z = [1.61, 1.53, 1.45, 1.35, 1.23, 1.10, 0.96, 0.79, 0.61, 0.42, 0.21] # (m)
v = [1.58, 1.95, 2.27, 2.69, 3.12, 3.49, 3.91, 4.38, 4.65, 4.91, 5.23] # (m/s)
m = 55E-3 # (kg) Masse de la balle
g = 9.81 # (m/s²) Accélération de la pesanteur
Epp = [m*g*z[i] for i in range(len(z))] # Tableau des énergies potentielles de pesanteur
Ec = [0.5*m*v[i]**2 for i in range(len(v))] # Tableau des énergies cinétiques
Em = [Epp[i]+Ec[i] for i in range(len(z))] # Tableau des énergies mécaniques
# AFFICHAGE
print("Epp (J) :", Epp)
print("Ec (J) :", Ec)
print("Em (J) :", Em)
>>> %Run
Epp (J) : [0.8686755000000002, 0.8255115000000002, 0.7823475000000001, 0.7283925000000001, 0.6636465000000001, 0.5935050000000002, 0.5179680000000001, 0.4262445000000001, 0.32912550000000007, 0.22661100000000003, 0.11330550000000002]
Ec (J) : [0.06865100000000002, 0.10456874999999999, 0.14170475, 0.19899275, 0.26769600000000005, 0.33495275, 0.42042275000000007, 0.527571, 0.5946187500000001, 0.66297275, 0.7522047500000002]
Em (J) : [0.9373265000000002, 0.9300802500000002, 0.9240522500000001, 0.9273852500000002, 0.9313425000000002, 0.9284577500000002, 0.9383907500000002, 0.9538155000000001, 0.9237442500000002, 0.88958375, 0.8655102500000003]
Exercice 7. (nombre de dilutions)
Cm = 1.0 # (g/L) Concentration solution mère
Cf = 1.0e-3 # (g/L) Concentration solution fille
Nb = 0 # Nombre de dilution (initialisation)
while Cm>Cf:
Nb = Nb + 1 # Incrémentation
Cm = Cm/10 # Dilution par 10
print("Il faut réaliser", Nb, "dilutions !")
>>> %Run
Il faut réaliser 3 dilutions !
La boucle doit s'arrêter quand Cm est égale ou inférieure à Cf !
Exercice 8. (avancement)
a, b, c, d = 1, 2, 3, 2 # coefficients stoechiométiques
n_A, n_B, n_C, n_D = 0.5, 0.5, 0, 0 # (mol) Quantités de matière initiales
x = 0 # Initialisation de l'avancement
dx = 0.01 # Pas de l'avancement
while (n_A>0 and n_B>0) :
x = x + dx # Incrémentation de l'avancement
n_A = n_A - a*dx # Décrémentation de n_A (réactif)
n_B = n_B - b*dx # Décrémentation de n_B (réactif)
n_C = n_C + c*dx # Incrémentation de n_C (produit)
n_D = n_D + d*dx # Incrémentation de n_D (produit)
# AFFICHAGE
print("xf = ", x)
print("n(A) = ", n_A)
print("n(B) = ", n_B)
print("n(C) = ", n_C)
print("n(D) = ", n_D)
>>> %Run
xf = 0.25000000000000006
n(A) = 0.24999999999999978
n(B) = -1.734723475976807e-16
n(C) = 0.7500000000000004
n(D) = 0.5000000000000001
Exercice 9. (dilution)
def dilution(Cm, Cf, Vf):
return Vf*Cf/Cm # Calcul de Vm
def dilution2(Cm, Cf, Vf):
Vm = Vf*Cf/Cm # Calcul de Vm
Veau = Vf-Vm # Calcul de Veau (volume d'eau à compléter)
F = Cm/Cf # Calcul du facteur de dilution
return Vm, Veau, F
>>> %Run
>>> dilution(30, 5, 100)
16.666666666666668
>>> Vm = dilution(30, 5, 100)
>>> Vm
16.666666666666668
>>> dilution2(30, 5, 100)
(16.666666666666668, 83.33333333333333, 6.0)
>>> Vm, Veau, F = dilution2(30, 5, 100)
>>> Vm
16.666666666666668
>>> Veau
83.33333333333333
>>> F
6.0
Exercice 10. (pH)
from math import log10
def potentiel_hydrogene(C_H3O_plus, C0 = 1):
return -log10(C_H3O_plus)/C0
def concentration_ion_hydronium(pH):
return 10**(-pH)
L'argument C0 fixé à 1 par défaut est optionnel.
>>> %Run
>>> potentiel_hydrogene(1E-5)
5.0
>>> potentiel_hydrogene(2E-5)
4.698970004336019
>>> potentiel_hydrogene(2E-5, C0=10) # N'a pas de sens ici !
0.4698970004336019
>>> concentration_ion_hydronium(7)
1e-07
>>> concentration_ion_hydronium(6.8)
1.584893192461114e-07
Exercice 11. (énergies)
import numpy as np
z = np.array([1.61, 1.53, 1.45, 1.35, 1.23, 1.10, 0.96, 0.79, 0.61, 0.42, 0.21]) # (m)
v = np.array([1.58, 1.95, 2.27, 2.69, 3.12, 3.49, 3.91, 4.38, 4.65, 4.91, 5.23]) # (m/s)
m = 55e-3 # (kg) Masse de la balle
g = 9.81 # (m/s²) Accélération de la pesanteur
Epp = m*g*z
Ec = 0.5*m*v**2
Em = Epp + Ec
# AFFICHAGE
print("Epp (J) :", Epp)
print("Ec (J) :", Ec)
print("Em (J) :", Em)
Les opérateurs sur les tableaux Numpy s'appliquent sur les éléments du même indice !
Pas besoin de faire des boucles avec les tableaux Numpy
>>> %Run
Epp (J) : [0.8686755 0.8255115 0.7823475 0.7283925 0.6636465 0.593505 0.517968
0.4262445 0.3291255 0.226611 0.1133055]
Ec (J) : [0.068651 0.10456875 0.14170475 0.19899275 0.267696 0.33495275
0.42042275 0.527571 0.59461875 0.66297275 0.75220475]
Em (J) : [0.9373265 0.93008025 0.92405225 0.92738525 0.9313425 0.92845775
0.93839075 0.9538155 0.92374425 0.88958375 0.86551025]
Exercice 12. (positions et vecteurs vitesse)
import matplotlib.pyplot as plt
x = [.014, .014, .014, .009, .009, .005, .005, .001, .001, .001, .003] # (m)
z = [1.61, 1.53, 1.45, 1.35, 1.23, 1.10, 0.96, 0.79, 0.61, 0.42, 0.21] # (m)
v = [1.58, 1.95, 2.27, 2.69, 3.12, 3.49, 3.91, 4.38, 4.65, 4.91, 5.23] # (m/s)
# FIGURE
plt.plot(x, z, "r+")
for i in range(len(x)):
plt.quiver(x[i], z[i], 0, -v[i], angles='xy', scale_units='xy', scale=30, color='blue', width=0.005)
plt.title("Chute d'une balle")
plt.xlabel("x (m)")
plt.xlim(-1,1)
plt.ylabel("y (m)")
plt.ylim(-0.2,1.8)
plt.grid()
plt.show()
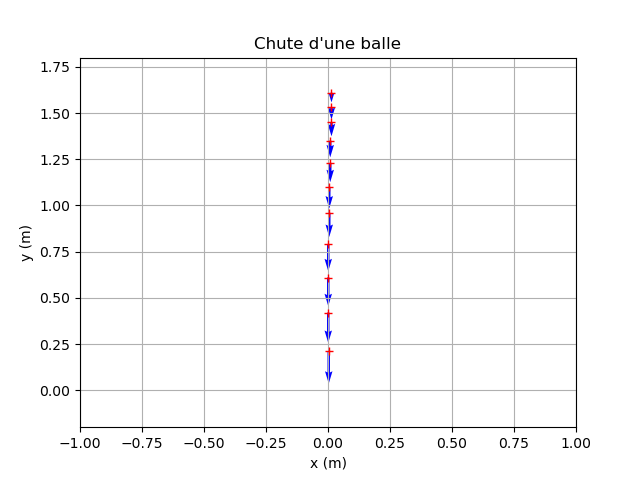
Exercice 13. (positions et vecteurs vitesse)
import matplotlib.pyplot as plt
# DONNEES
t = [0.0, 0.0667, 0.1334, 0.2001, 0.2668, 0.3335, 0.4002, 0.4669, 0.5336, 0.6003, 0.667, 0.7337, 0.8004, 0.8671, 0.9338]
x = [0.003, 0.141, 0.275, 0.410, 0.554, 0.686, 0.820, 0.958, 1.089, 1.227, 1.359, 1.490, 1.599, 1.705, 1.801]
y = [0.746, 0.990, 1.175, 1.336, 1.432, 1.505, 1.528, 1.505, 1.454, 1.355, 1.207, 1.018, 0.797, 0.544, 0.266]
# INITIALISATION
N = len(t) # Taille
vx = [0]*N # Liste de N zéros
vy = [0]*N # Liste de N zéros
# CALCULS
for i in range(1, N-1):
vx[i] = (x[i+1]-x[i-1])/(t[i+1]-t[i-1]) # Calcul de la composante vx
vy[i] = (y[i+1]-y[i-1])/(t[i+1]-t[i-1]) # Calcul de la composante vy
# AFFICHAGE
print("vx :", vx)
print("vy :", vx)
# FIGURE
plt.plot(x, y, "r+")
for i in range(1, N-1):
plt.quiver(x[i], y[i], vx[i], vy[i], angles='xy', scale_units='xy', scale=20, color='blue', width=0.005)
plt.title("Lancé d'une balle")
plt.xlabel("x (m)")
plt.xlim(0,2)
plt.ylabel("y (m)")
plt.ylim(0,1.8)
plt.grid()
plt.show()
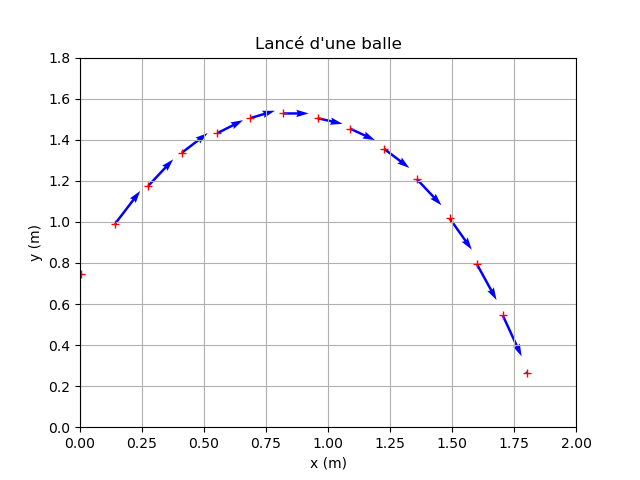
>>> %Run Exo13.py
vx : [0, 2.038980509745128, 2.0164917541229386, 2.0914542728635683, 2.0689655172413794, 1.9940029985007486, 2.0389805097451275, 2.016491754122939, 2.01649175412294, 2.0239880059970004, 1.9715142428785588, 1.7991004497751129, 1.6116941529235393, 1.5142428785607198, 0]
vy : [0, 2.038980509745128, 2.0164917541229386, 2.0914542728635683, 2.0689655172413794, 1.9940029985007486, 2.0389805097451275, 2.016491754122939, 2.01649175412294, 2.0239880059970004, 1.9715142428785588, 1.7991004497751129, 1.6116941529235393, 1.5142428785607198, 0]
Exercice 14. (histogramme et incertitude-type)
import matplotlib.pyplot as plt
import statistics as stat
# répétabilité de la mesure d'un volume équivalent pour plusieurs groupes
f = [19.1, 18.9, 18.7, 19.0, 18.9, 19.2, 18.8, 18.7] # Listes des mesures
# HISTOGRAMME
freq, x, _ = plt.hist(f, range=(18, 20), bins=10, rwidth=0.95)
plt.title("Fréquence des mesures de la distance focale d'une lentille")
plt.grid(axis='y')
plt.xticks(x)
plt.show()
# CALCULS
N = len(f)
f_moy = stat.mean(f)
s = stat.stdev(f)
ua_f = s/stat.sqrt(N)
# AFFICHAGE
print("f_prime = ", round(f_moy,2), "+/-", round(ua_f,2), "mm")
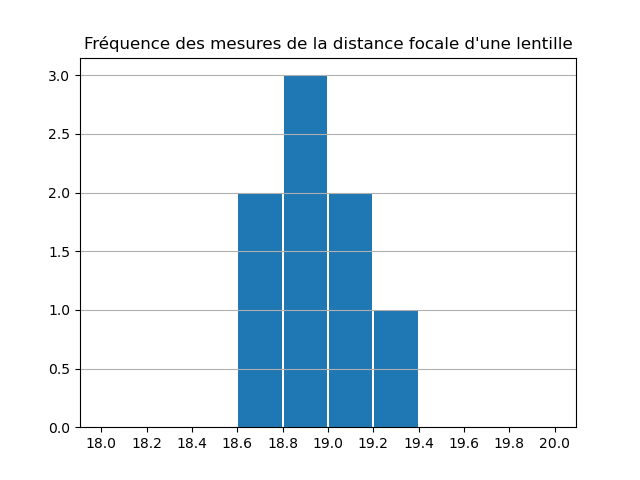
>>> %Run
f_prime = 18.91 +/- 0.06 mm