Mouvement d'un point : vecteur variation vitesse
Programme de première générale - Enseignement de spécialité - 2019
"Utiliser un langage de programmation pour étudier la relation approchée entre la variation du vecteur vitesse d’un système modélisé par un point matériel entre deux instants voisins et la somme des forces appliquées sur celui-ci".
Principe
Vitesse moyenne \(v_i\) en un point \(M_i\) entre deux positions proches :
\[v_i = \dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}\]
Le vecteur variation vitesse \(\Delta\vec{v}_i\) au point \(M_i\) est défini par :
\[\Delta\vec{v}_i = \vec{v}_{i+1} - \vec{v}_{i-1}\]
Pour un système de masse \(m\) soumis à une ou plusieurs forces :
\[\boxed{\Sigma\vec{F} = m \times \dfrac{\Delta\vec{v}}{\Delta t}}
\hspace{1cm}\text{avec}\hspace{1cm}
\Delta = t_{i+1}-t_{i-1}\]
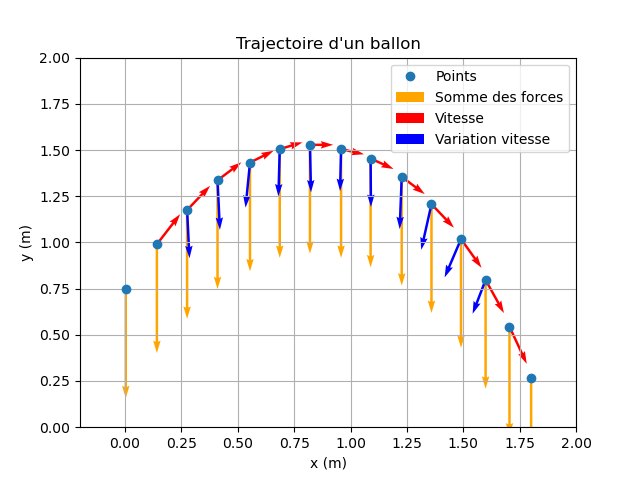
Exemple : lancé d'un ballon
import matplotlib.pyplot as plt
from math import sqrt
# MESURES
t = [0.000, 0.066, 0.132, 0.198, 0.264, 0.330, 0.396, 0.462, 0.528, 0.594, 0.660, 0.726, 0.792, 0.858, 0.924]
x = [0.003, 0.141, 0.275, 0.410, 0.554, 0.686, 0.820, 0.958, 1.089, 1.227, 1.359, 1.490, 1.599, 1.705, 1.801]
y = [0.746, 0.990, 1.175, 1.336, 1.432, 1.505, 1.528, 1.505, 1.454, 1.355, 1.207, 1.018, 0.797, 0.544, 0.266]
N = len(x)
# CALCUL DES VITESSES
vx = [0 for i in range(N)]
vy = [0 for i in range(N)]
for i in range(1, N-1):
vx[i] = (x[i+1]-x[i-1])/(t[i+1]-t[i-1])
vy[i] = (y[i+1]-y[i-1])/(t[i+1]-t[i-1])
# CALCUL DES VARIATIONS VITESSE
dvx = [0 for i in range(N)]
dvy = [0 for i in range(N)]
for i in range(2, N-2):
dvx[i] = vx[i+1]-vx[i-1]
dvy[i] = vy[i+1]-vy[i-1]
dv = [round(sqrt(dvx[i]**2+dvy[i]**2),2) for i in range(N)]
print("Dv = ", dv)
# CALCUL DES SOMMES DES FORCES (poids uniquement)
m = 0.3
g = 9.81
Fx = [0 for i in range(N)]
Fy = [-m*g for i in range(N)]
# FIGURES
plt.plot(x, y, "o", label="Points")
plt.quiver(x, y, Fx, Fy, angles='xy', scale_units='xy', scale=5, color='orange', width=0.005, label="Somme des forces")
plt.quiver(x, y, vx, vy, angles='xy', scale_units='xy', scale=20, color='red', width=0.005, label="Vitesse")
plt.quiver(x, y, dvx, dvy, angles='xy', scale_units='xy', scale=5, color='blue', width=0.005, label="Variation vitesse")
plt.legend()
plt.title("Trajectoire d'un ballon")
plt.xlabel("x (m)")
plt.xlim(-0.2, 2)
plt.ylabel("y (m)")
plt.ylim(0, 2)
plt.grid()
plt.show()
La fonction
quiver()permet de tracer un vecteur ou un champ de vecteur à partir de listes.
- Résultats