Bilan énergétique d'un mouvement

Programme de première générale - Enseignement de spécialité - 2019

"Utiliser un langage de programmation pour effectuer le bilan énergétique d’un système en mouvement".

Principe

Calculer à partir de données expérimentales ou de façon théorique l'énergie cinétique et l'énergie potentielle de pesanteur d'un système en mouvement.

\[E_c = \dfrac{1}{2} m~v^2 \hspace{100px} E_{pp} = m~g~h\]

Mettre en évidence la conservation ou la non-conservation de l'énergie mécanique.

\[E_m = E_c + E_{pp}\]

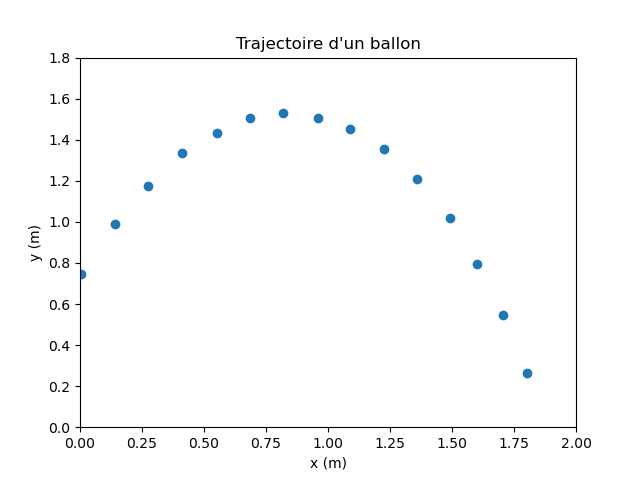
Exemple 1 : lancé d'un ballon

La trajectoire expérimentale d'un ballon est donnée par la figure suivante :

Trajectoire d'un ballon 
import matplotlib.pyplot as plt

# DONNEES EXPERIMENTALES (v a été calculée à partir des positions x et y)
x = [0.141, 0.275, 0.410, 0.554, 0.686, 0.820, 0.958, 1.089, 1.227, 1.359, 1.490, 1.599, 1.705]
t = [0.066, 0.132, 0.198, 0.264, 0.330, 0.396, 0.462, 0.528, 0.594, 0.660, 0.726, 0.792, 0.858]
v = [3.848, 3.320, 2.874, 2.452, 2.142, 2.061, 2.114, 2.333, 2.772, 3.238, 3.599, 3.943, 4.304]
z = [0.990, 1.175, 1.336, 1.432, 1.505, 1.528, 1.505, 1.454, 1.355, 1.207, 1.018, 0.797, 0.544]

# PARAMETRES
m = 0.3  # (kg)
g = 9.81 # (m/s²)

# CALCULS
N = len(v)                               # Taille des tableaux
Ec  = [0.5*m*v[i]**2 for i in range(N)]  # Calcul de Ec
Epp = [m*g*z[i] for i in range(N)]       # Calcul de Epp
Em  = [Ec[i] + Epp[i] for i in range(N)] # Calcul de Em

# TRACES DES COURBES
plt.plot(x, Ec,  "+-", label="Ec")
plt.plot(x, Epp, "+-", label="Epp")
plt.plot(x, Em,  "+-", label="Em")
plt.legend()
plt.title("Bilan énergétique du lancé d'un ballon (m = 300 g)")
plt.xlabel("x (m)")
plt.xlim(0, 2)
plt.ylabel("Energies (J)")
plt.ylim(0, 6)
plt.grid()
plt.show()
Résultats

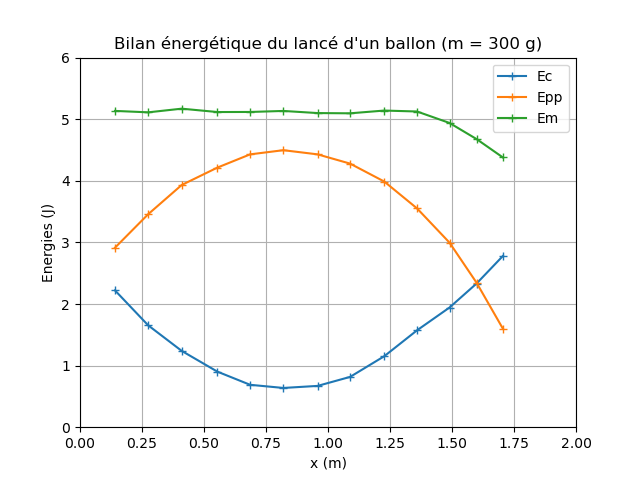
Animation propagation onde

Exemple 2 : saut à l'élastique

D'après un document Eduscol.

Début de la chute (élastique non tendu)

La hauteur de chute \(h\) (grandeur positive) est la distance entre l'objet de masse \(m\) en chute libre et le pont. La hauteur entre le pont et le sol est \(h_0 = 80~\rm m\).

L'altitude \(z\) du pont est prise comme référence d'où :

\[E_{pp} = m~g~z = -m~g~h\]

Par conservation de l'énergie mécanique on en déduit :

\[E_{c} = E_m - E_{pp} \hspace{50px}\text{avec}\hspace{50px} E_{m} = 0~\rm J \hspace{20px}\text{(conditions initiales)}\]
import matplotlib.pyplot as plt

# PARAMETRES
m = 60            # (kg)   Masse
g = 9.81          # (m/s²) Accélération de la pesanteur
h0 = 80           # (m)    Hauteur de la chute entre le pont et le sol

# INITIALISATION
h_chute = []      # (m) Tableau vide des hauteurs de chute
E_pp = []         # (J) Tableau vide des énergies potentielles de pesanteur
E_c = []          # (J) Tableau vide des énergies cinéitiques



# CALCULS DES ENERGIES
Em = 0            # (J) Energie mécanique aux conditions initiales
h = 0             # (m) Hauteur de chute initiale
pas = 1           # (m) Pas d'incrémentation de la hauter de chute
while h <= h0:
   Epp = -m*g*h           # Calcul Epp
   Ec = Em - Epp          # Calcul Ec par conservation de l'énergie mécanique
   E_pp.append(Epp)       # Complète le tableau E_pp
   E_c.append(Ec)         # Complète le tableau E_c
   h_chute.append(h)      # Complète le tableau des hauteurs de chute
   h = h + pas            # Incrémente la hauteur

E_m = [E_c[i]+E_pp[i] for i in range(len(E_c))]  # Vérification de l'énergie mécanique

# COURBES
plt.subplots_adjust(left=0.17)             # Marge de 17% à gauche pour meilleur affichage
plt.plot(h_chute, E_pp, "+-", label="Epp")  # Courbe de Epp
plt.plot(h_chute, E_c,  "+-", label="Ec")   # Courbe de Ec
plt.plot(h_chute, E_m,  "+-", label="Em")   # Courbe de Em
plt.title("Saut à l'élastique (élastique non tendu)")
plt.xlabel("Hauteur de chute (m)")
plt.ylabel("Energies (J)")
plt.legend()
plt.grid()
plt.show()
Résultats

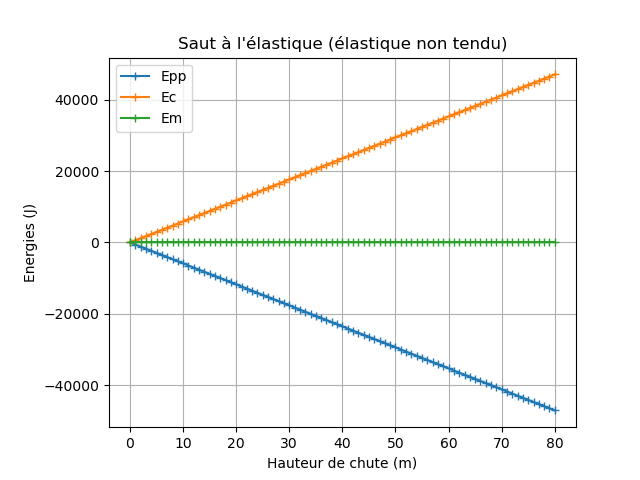
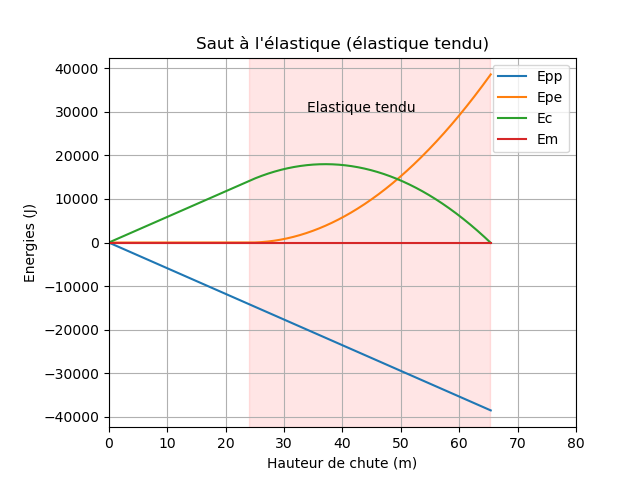
alternate text

Chute complète (élastique tendu)

En tenant compte de l'action de l'élastique pour une distance supérieure à sa longueur à vide \(l_0 = 24~\rm m\).

L'énergie potentielle élastique s'écrit :

\[E_{pe} = \dfrac{1}{2}~k~(h-l_0)^2\]

Par conservation de l'énergie mécanique on en déduit :

\[E_{c} = E_m - E_{pp} - E_{pe} \hspace{50px}\text{avec}\hspace{50px} E_{m} = 0~\rm J \hspace{20px}\text{(conditions initiales)}\]
import matplotlib.pyplot as plt

# PARAMETRES
m = 60            # (kg)   Masse
g = 9.81          # (m/s²) Accélération de la pesanteur
h0 = 80           # (m)    Hauteur de la chute entre le pont et le sol
l0 = 24           # (m)     Longueur de l'élastique
k = 45            # (N.m-1) Constante d'élasticité

# INITIALISATION
h_chute = []      # (m) Tableau vide des hauteurs de chute
E_pp = []         # (J) Tableau vide des énergies potentielles de pesanteur
E_pe = []         # (J) Tableau vide des énergies potentielles élastiques
E_c = []          # (J) Tableau vide des énergies cinéitiques



# CALCULS DES ENERGIES
Em = 0            # (J) Energie mécanique aux conditions initiales
h = 0             # (m) Hauteur de chute initiale
pas = 1           # (m) Pas d'incrémentation de la hauter de chute
while h <= h0:
   Epp = -m*g*h               # Calcul Epp
   if h<l0:
      Epe = 0                # Epe (élastique non tendu)
   else:
      Epe = 0.5*k*(h-l0)**2  # Caclul Epe (élastique tendu)
   Ec = Em - Epp - Epe
   E_pp.append(Epp)           # Complète le tableau E_pp
   E_pe.append(Epe)           # Complète le tableau E_pe
   E_c.append(Ec)             # Complète le tableau E_c par conservation de l'énergie mécanique
   h_chute.append(h)          # Complète le tableau des hauteurs de chute
   h = h + pas                # Incrémente la hauteur

E_m = [E_c[i]+E_pp[i]+E_pe[i] for i in range(len(E_c))]  # Vérification de l'énergie mécanique

# COURBES
plt.subplots_adjust(left=0.17)             # Marge de 17% à gauche pour meilleur affichage
plt.plot(h_chute, E_pp, "+-", label="Epp")  # Courbe de Epp
plt.plot(h_chute, E_pe, "+-", label="Epe")  # Courbe de Epe
plt.plot(h_chute, E_c,  "+-", label="Ec")   # Courbe de Ec
plt.plot(h_chute, E_m,  "+-", label="Em")   # Courbe de Em
plt.axvspan(l0, h0, color='r', alpha=0.1) # Zone où l'élastique est tendu
plt.text(40, 5E4, "Elastique tendu")
plt.title("Saut à l'élastique (élastique tendu)")
plt.xlabel("Hauteur de chute (m)")
plt.ylabel("Energies (J)")
plt.legend()
plt.grid()
plt.show()
Résultats

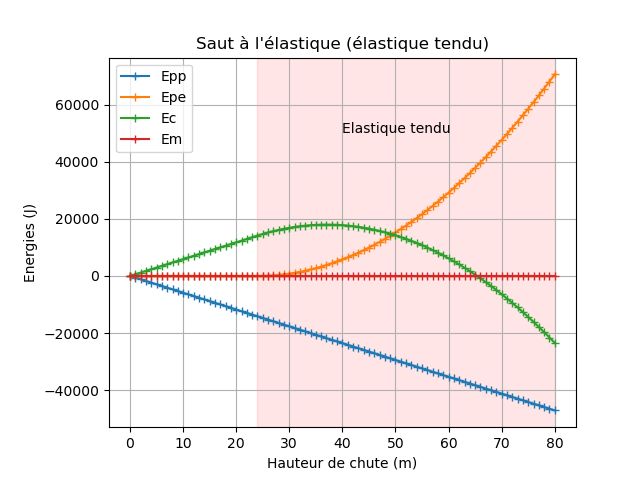
alternate text
Questionnement

  • Quelle est la vitesse maximale de la chute ?

  • Est-il possible physiquement d'obtenir une énergie cinétique négative ?

  • Ce saut à l'élastique est-il sûr ? Quelle est la hauteur maximale de la chute ?

  • Modifier le code pour obtenir la hauteur maximale.

Détermination de la hauteur maximale

Il suffit d'ajouter une condition supplémentaire sur une énergie cinétique toujours positive ou nulle.

La hauteur maximale est la dernière valeur du tableau des hauteurs (avant dernière en réalité).

import matplotlib.pyplot as plt

# PARAMETRES
m = 60            # (kg)   Masse
g = 9.81          # (m/s²) Accélération de la pesanteur
h0 = 80           # (m)    Hauteur de la chute entre le pont et le sol
l0 = 24           # (m)     Longueur de l'élastique
k = 45            # (N.m-1) Constante d'élasticité

# INITIALISATION
h_chute = []      # (m) Tableau vide des hauteurs de chute
E_pp = []         # (J) Tableau vide des énergies potentielles de pesanteur
E_pe = []         # (J) Tableau vide des énergies potentielles élastiques
E_c = []          # (J) Tableau vide des énergies cinéitiques



# CALCULS DES ENERGIES
Em = 0            # (J) Energie mécanique aux conditions initiales
Ec = 0            # (J) Energie cinétique initiale
h = 0             # (m) Hauteur de chute initiale
pas = 0.1         # (m) Pas d'incrémentation de la hauter de chute
while h<=h0 and Ec>=0:
   Epp = -m*g*h               # Calcul Epp
   if h<l0:
      Epe = 0                # Epe (élastique non tendu)
   else:
      Epe = 0.5*k*(h-l0)**2  # Caclul Epe (élastique tendu)
   Ec = Em - Epp - Epe
   E_pp.append(Epp)           # Complète le tableau E_pp
   E_pe.append(Epe)           # Complète le tableau E_pe
   E_c.append(Ec)             # Complète le tableau E_c par conservation de l'énergie mécanique
   h_chute.append(h)          # Complète le tableau des hauteurs de chute
   h = h + pas                # Incrémente la hauteur

hmax = h_chute[-2]  # La hauteur maximale est avant dernière vauleur
print("La hauteur maximale de la chute est de", round(hmax,1), "m")

E_m = [E_c[i]+E_pp[i]+E_pe[i] for i in range(len(E_c))]  # Vérification de l'énergie mécanique

# COURBES
plt.subplots_adjust(left=0.17)             # Marge de 17% à gauche pour meilleur affichage
plt.plot(h_chute, E_pp, "-", label="Epp")  # Courbe de Epp
plt.plot(h_chute, E_pe, "-", label="Epe")  # Courbe de Epe
plt.plot(h_chute, E_c,  "-", label="Ec")   # Courbe de Ec
plt.plot(h_chute, E_m,  "-", label="Em")   # Courbe de Em
plt.axvspan(l0, hmax, color='r', alpha=0.1) # Zone où l'élastique est tendu
plt.text(l0+10, 3E4, "Elastique tendu")
plt.title("Saut à l'élastique (élastique tendu)")
plt.xlabel("Hauteur de chute (m)")
plt.ylabel("Energies (J)")
plt.xlim(0, h0)
plt.legend()
plt.grid()
plt.show()
Résultats

>>> %Run
La hauteur maximale de la chute est de 65.3 m
alternate text