Représentation d'une onde
Programme de première générale - Enseignement de spécialité - 2019
"Représenter un signal périodique et illustrer l’influence de ses caractéristiques (période, amplitude) sur sa représentation".
Principe
Tracer un signal sinusoïdal décrit par l'expression :
\[s(t) = A \times \cos(\dfrac{2\pi}{T}\cdot t)\]
Montrer l'influence de la période et de l'amplitude.
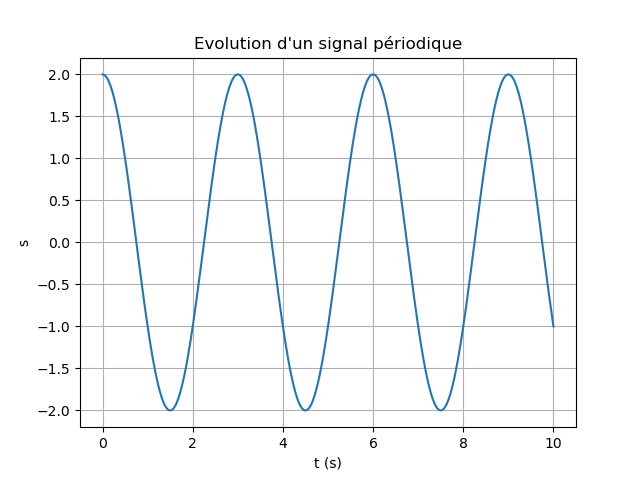
Exemple 1 : pour une amplitude et une période
Une simple représentation d'un signal sinusoïdal.
Les valeurs des variables A (amplitude) et T (période) sont à modifier pour montrer leurs influences.
import numpy as np
import matplotlib.pyplot as plt
from math import pi
# DEFINTION DES CONSTANTES
A = 2 # Amplitude
T = 3 # Période (s)
# CALCULS
t = np.linspace(0, 10, 500) # Tableau des valeurs du temps en seconde
s = A*np.cos(2*pi*t/T) # Tableau des valeurs calculées du signal sinusoïdal
# COURBES
plt.plot(t, s)
plt.title("Evolution d'un signal périodique")
plt.xlabel("t (s)")
plt.ylabel("s")
plt.grid()
plt.savefig("premiere_signal_sinusoidal_1.png")
plt.show()
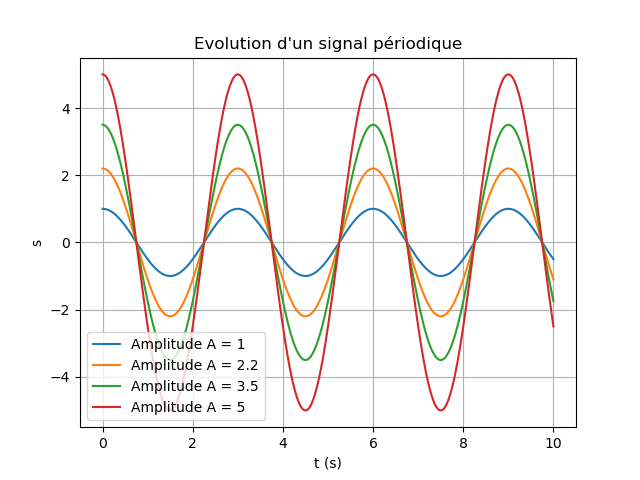
Exemple 2 : pour plusieurs amplitudes
Tracer plusieurs signaux sinusoïdaux pour des amplitudes différentes placée dans une liste à modifier !
import numpy as np
import matplotlib.pyplot as plt
from math import pi
# DEFINTION DES CONSTANTES
T = 3 # Période (s)
# CALCULS
t = np.linspace(0, 10, 500) # Tableau des valeurs du temps en seconde
# COURBES
for A in [1, 2.2, 3.5, 5]:
s = A*np.cos(2*pi*t/T) # Tableau des valeurs calculées du signal sinusoïdal
plt.plot(t, s, label="Amplitude A = " + str(A))
plt.legend()
plt.title("Evolution d'un signal périodique")
plt.xlabel("t (s)")
plt.ylabel("s")
plt.grid()
plt.show()
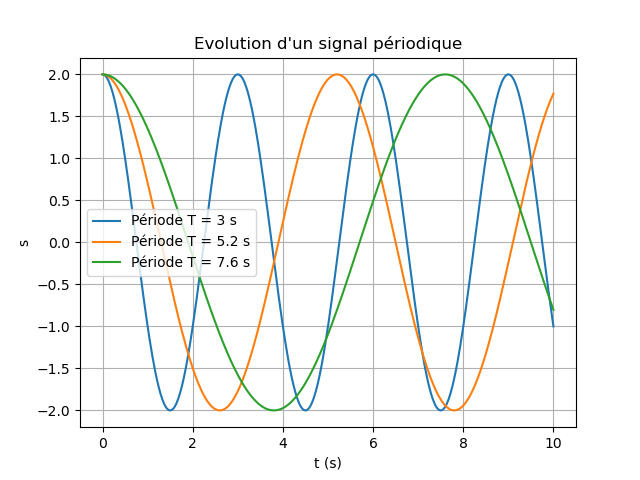
Exemple 3 : pour plusieurs périodes
Tracer plusieurs signaux sinusoïdaux pour des périodes différentes placée dans une liste à modifier !
import numpy as np
import matplotlib.pyplot as plt
from math import pi
# DEFINTION DES CONSTANTES
A = 2 # Amplitude
# CALCULS
t = np.linspace(0, 10, 500) # Tableau des valeurs du temps en seconde
# COURBES
for T in [3, 5.2, 7.6]:
s = A*np.cos(2*pi*t/T) # Tableau des valeurs calculées du signal sinusoïdal
plt.plot(t, s, label="Période T = " + str(T) + " s")
plt.legend()
plt.title("Evolution d'un signal périodique")
plt.xlabel("t (s)")
plt.ylabel("s")
plt.grid()
plt.show()
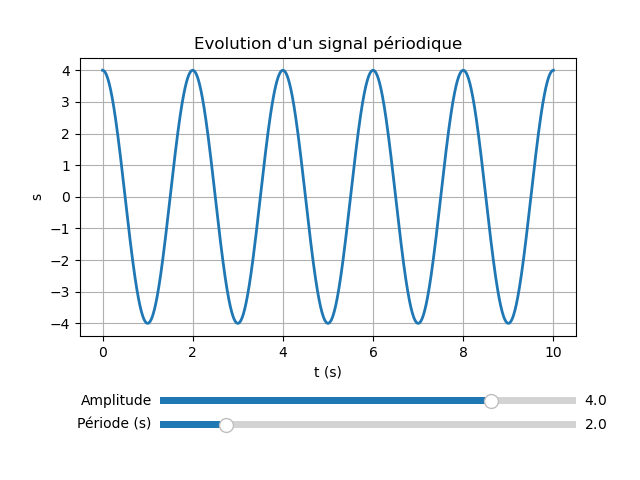
Exemple 4 : avec des curseurs
Modifier l'amplitude et/ou la période à l'aide de la souris avec des curseurs (sliders).
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider # Curseur
from math import pi
# DEFINITION DES CONSTANTES
A = 4 # Amplitude initiale
T = 2 # Période initiale
dT = 0.1 # Pas de variation de la période
# CALCULS
t = np.linspace(0, 10, 1000) # Tableau des valeurs du temps en seconde
s = A*np.cos(2*pi*t/T) # Tableau des valeurs calculées du signal sinusoïdal
# COURBE
fig, ax = plt.subplots() # Zone de dessin
plt.subplots_adjust( bottom=0.30) # Laisse une marge de 30% en bas de la zone de dessin pour placement des curseurs
trace, = plt.plot(t, s, lw=2) # Trace le signal s(t) et récupère le tracé
plt.title("Evolution d'un signal périodique") # Titre
plt.xlabel("t (s)") # Légende axe x
plt.ylabel("s") # Légende axe y
plt.grid() # Affiche la grille
# AJOUT DES CURSEURS
ax_periode = plt.axes([0.25, 0.1, 0.65, 0.03], facecolor='lightgoldenrodyellow') # Zone de placement du curseur période
ax_amp = plt.axes([0.25, 0.15, 0.65, 0.03], facecolor='lightgoldenrodyellow') # Zone de placement du curseur amplitude
s_periode = Slider(ax_periode, 'Période (s)', 0.5, 10.0, valinit=T, valstep=dT) # Paramétrage du curseur période
s_amp = Slider(ax_amp, 'Amplitude', 0.1, 5, valinit=A) # Paramétrage du curseur amplitude
def update(val):
""" Fonction d'actulisation de la courbe """
A = s_amp.val # Récupération de la nouvelle amplitude
T = s_periode.val # Récupération de la nouvelle période
trace.set_ydata(A*np.cos(2*pi*t/T)) # Calcul du nouveau signal
fig.canvas.draw_idle() # Dessine la nouvelle courbe
s_periode.on_changed(update) # Lance la fonction update(val) si le curseur période change !
s_amp.on_changed(update) # Lance la fonction update(val) si le curseur amplitude change !
plt.show()