Evolution temporelle d'une transformation chimique

Programme de classe terminale, enseignement de spécialité, voie générale

À l’aide d’un langage de programmation et à partir de données expérimentales, tracer l’évolution temporelle d’une concentration, d’une vitesse volumique d’apparition ou de disparition et tester une relation donnée entre la vitesse volumique de disparition et la concentration d’un réactif.

Simulation de la disparition d'un espèce chimique

Principe

Dans une réaction chimique d'ordre 1, la vitesse volumique de disparition d'un réactif R est proportionnelle à sa concentration [R] au cours du temps.

\[v_{disp}(R) = k \times [R] \quad\text{avec}\quad v_{disp}(R) = - \dfrac{d[R]}{dt}\]

\(k\) est la constante de vitesse.

Le calcul de la vitesse est donnée par l'expression :

\[v_{disp}(R) = \dfrac{C_{n+1}-C_{n}}{t_{n+1}-t_{n}} \quad\text{en posant}\quad C = [R]\]

Il est donc possible de tracer l'évolution de la concentration du réactif en fonction de temps de proche en proche à partir de la relation :

\[C_{n+1} = C_{n} - k \times (t_{n+1}-t_{n}) \times C_{n}\]

Programme Python

import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"] = (8,6)  # width, height in inches (100 dpi)

Dt = 0.2
N = 50
t = [Dt*i for i in range(N)]
C = [0]*N

C[0] = 1.000
k = 0.464

for i in range(N-1):
   C[i+1] = C[i] - (t[i+1]-t[i])*k*C[i]

plt.plot(t, C, "o")
plt.title("Evolution temporelle d'un système chimique")
plt.xlabel("t (s)")
plt.xlim(0, 10)
plt.ylabel("Concentration (mol/L)")
plt.ylim(0, 1)
plt.grid()
plt.show()
Résultats

alternate text

Animation

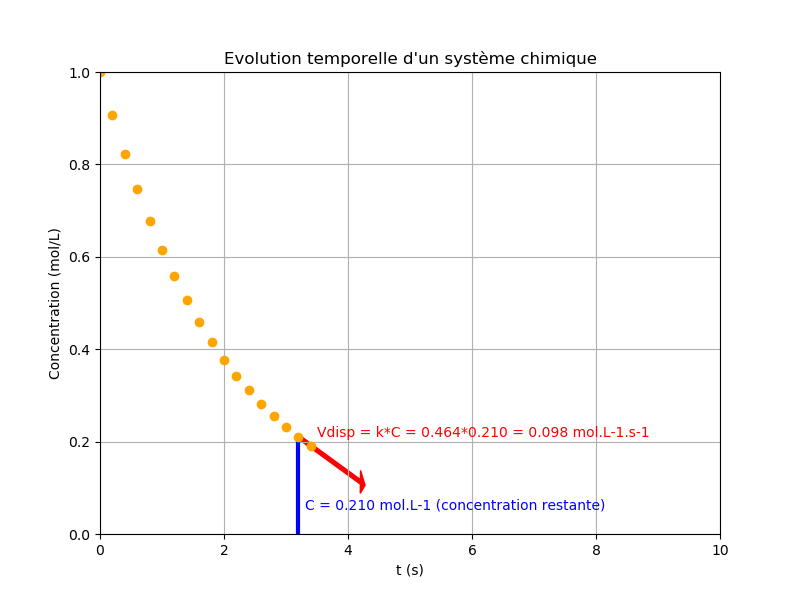
Le programme suivant trace les points de la courbe pas à pas en mettant en évidence à chaque fois la concentration restante en solution et le vecteur vitesse de disparition ( \(v_{disp} = -k \times C_{n}\)).

Ici une boucle while (avec une condition sur la concentration) est utilisée à la place d'un for !

import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"] = (8,6)  # width, height in inches (100 dpi)

Dt = 0.2    # Pas temporel
k = 0.464   # Constante de vitesse

t = [0]     # Tableau du temps initialisé à 0
C = [1.000] # Tableau des concentrations initialisé à Co
Clim = 0.2  # Concentration qui arrête la boucle while



while C[-1] > Clim :
   # Calculs
   a = k*C[-1]                             # Calcul de la vitesse
   t.append(t[-1]+Dt)                      # Ajoute tn+1 dans le tableau des temps
   C.append(C[-1] - (t[-1]-t[-2])*k*C[-1]) # Calcul de Cn+1 et ajout dans tableau des concentrations

   # Efface la figure
   plt.clf()

   # Tracé de la concentration restante
   plt.plot([t[-2], t[-2]], [0, C[-2]], color='blue', linewidth=3)
   plt.text(t[-2]+0.1, C[-2]/4, "C = {:.3f} mol.L-1 (concentration restante)".format(C[-2]), color='blue')

   # Tracé du vecteur vitesse (tangente)
   plt.arrow(t[-2], C[-2], 1, -a ,color='red', width=0.01, head_width=0.05)
   plt.text(t[-2]+0.3, C[-2], "Vdisp = k*C = {:.3f}*{:.3f} = {:.3f} mol.L-1.s-1".format(k, C[-2], k*C[-2]), color='red')

   # Tracé des points de la courbe
   plt.plot(t, C, "o", color="orange")

   # Autres
   plt.title("Evolution temporelle d'un système chimique")
   plt.xlabel("t (s)")
   plt.xlim(0, 10)
   plt.ylabel("Concentration (mol/L)")
   plt.ylim(0, 1)
   plt.grid()

   # Pause
   plt.pause(2)

#plt.savefig("evolution_temporelle_disparition_anim.png")
plt.show()
Résultats

alternate text