Seconde loi de Kepler

Programme de classe terminale, enseignement de spécialité, voie générale

Exploiter, à l’aide d’un langage de programmation, des données astronomiques ou satellitaires pour tester les deuxième et troisième lois de Kepler.

Principe

Soit une planète en orbite elliptique autour du soleil dans le référentiel héliocentrique supposé galiléen.

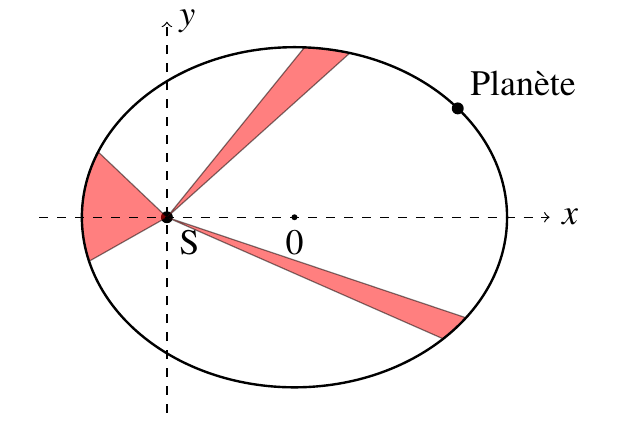
La seconde loi de Kepler suppose que les aires balayées sont égales pendant des durées égales.

La formule de Heron donne une estimation de cette aire à partir d'une forme triangulaire.

\[A = \sqrt{p(p-L_1)(p-L_2)(p-L_3)} \hspace{1cm}\text{avec}\hspace{1cm} p = \dfrac{L_1+L_2+L_3}{2}\]

Exemple : cas de Neptune

Dans cet exemple, les positions x et y (en ua) de Neptune par rapport au soleil sont données pour les années 2020 à 2024.

import matplotlib.pyplot as plt
from math import sqrt

# Positon de Neptune
t = [2020, 2021, 2022, 2023, 2024] # années
x = [29.4328410560730, 29.6118356847488, 29.7457682031831, 29.8342404541355, 29.8774316380940] # en ua
y = [-5.3906071859853, -4.2505317595919, -3.1034908723970, -1.9519995345194, -0.7985426911486] # en ua

def aire_balayee(x1, y1, x2, y2):
   """ Retourne l'aire balayée entre deux points par la méthode de Heron
   """
   L1 = sqrt(x1**2 + y2**2)
   L2 = sqrt(x2**2 + y2**2)
   L3 = sqrt((x2-x1)**2 + (y2-y1)**2)
   p = (L1+L2+L3)/2
   return sqrt(p*(p-L1)*(p-L2)*(p-L3))

Dt = []
aire = []
for i in range(len(x)-1):
   Dt.append(t[i+1]-t[i])
   aire.append(aire_balayee(x[i], y[i], x[i+1], y[i+1]))

print("Delta t (an) :\n", Dt)
print("Aire balayée (ua2) :\n", aire)

Résultats

>>> %Run script.py
Delta t (an) :
[1, 1, 1, 1]
Aire balayée (ua2) :
[17.00345082200997, 17.112266685090646, 17.185248384788228, 17.22165946734367]

On vérifie que les aires balayées sont pratiquement égales !